THE KISS PRECISE
By:
February 17, 2025
A (pro- or anti-) science-, mathematics-, technology-, space-, apocalypse-, dehumanization-, disenchantment-, and/or future-oriented poem published during sf’s emergent Radium Age (c. 1900–1935). Research and selection by Joshua Glenn.
For pairs of lips to kiss maybe
Involves no trigonometry.
‘Tis not so when four circles kiss
Each one the other three.
To bring this off the four must be
As three in one or one in three.
If one in three, beyond a doubt
Each gets three kisses from without.
If three in one, then is that one
Thrice kissed internally.
Four circles to the kissing come.
The smaller are the benter.
The bend is just the inverse of
The distance from the center.
Though their intrigue left Euclid dumb
There’s now no need for rule of thumb.
Since zero bend’s a dead straight line
And concave bends have minus sign,
The sum of the squares of all four bends
Is half the square of their sum.
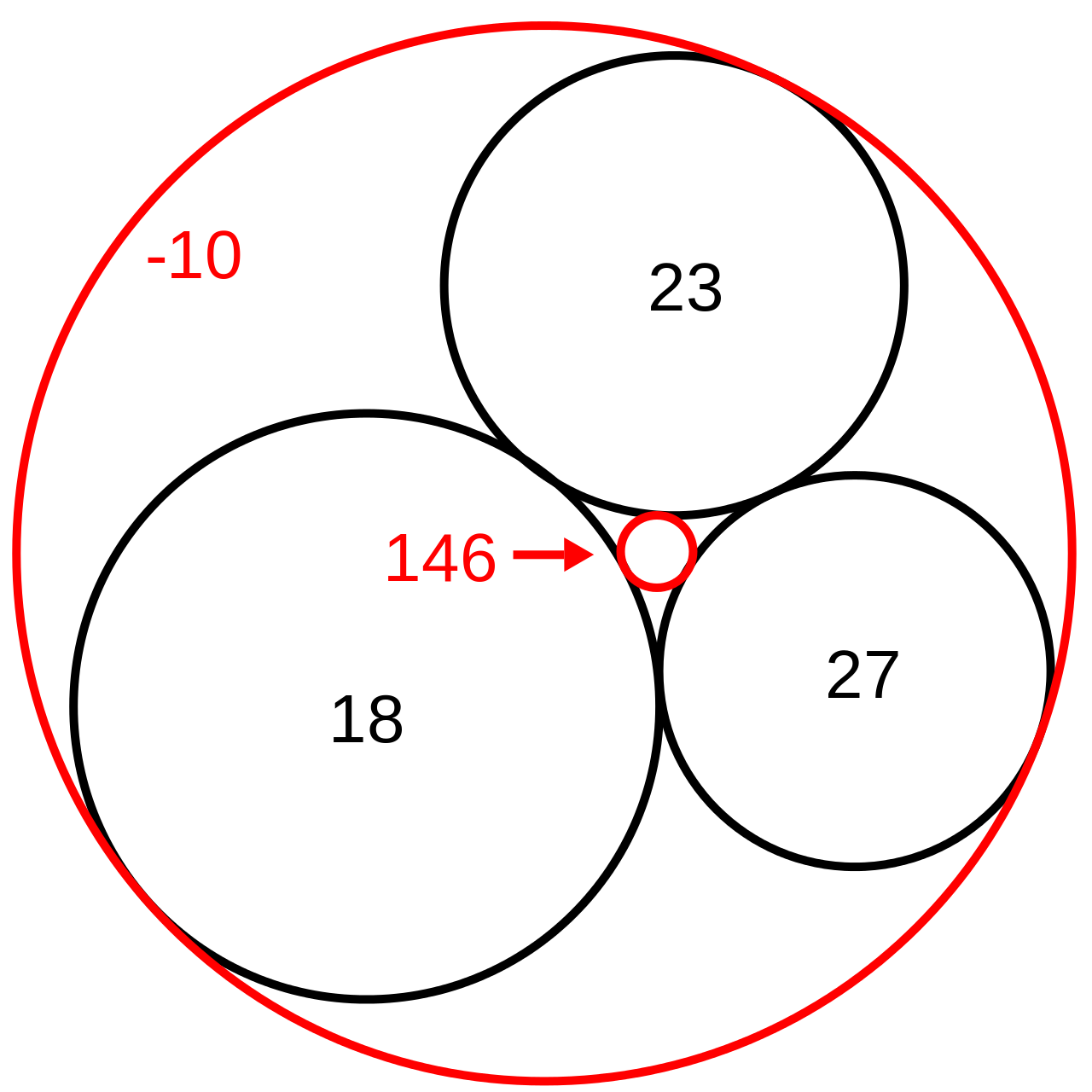
— In Euclidean plane geometry, Apollonius’s problem is to construct circles that are tangent to three given circles in a plane. René Descartes gave a formula relating the radii of the solution circles and the given circles, now known as Descartes’ theorem. Descartes’ theorem was rediscovered independently in 1936 by Frederick Soddy — the English radiochemist who explained, with Ernest Rutherford, that radioactivity is due to the transmutation of elements, now known to involve nuclear reactions. Soddy published his findings in a 1936 issue of the scientific journal Nature as a poem, of which the first two stanzas are reproduced here.
The first stanza describes Soddy’s circles, whereas the second stanza gives Descartes’ theorem. In Soddy’s poem, two circles are said to “kiss” if they are tangent, whereas the term “bend” refers to the curvature k of the circle.
If the three given circles are mutually tangent, Apollonius’ problem has five solutions. Three solutions are the given circles themselves, since each is tangent to itself and to the other two given circles. The remaining two solutions (shown in red here) correspond to the inscribed and circumscribed circles, and are called Soddy’s circles.
RADIUM AGE PROTO-SF POETRY: Stephen Spender’s THE PYLONS | George Sterling’s THE TESTIMONY OF THE SUNS | Archibald MacLeish’s EINSTEIN | Thomas Thornely’s THE ATOM | C.S. Lewis’s DYMER | Stephen Vincent Benét’s METROPOLITAN NIGHTMARE | Robert Frost’s FIRE AND ICE | Aldous Huxley’s FIFTH PHILOSOPHER’S SONG | Sara Teasdale’s “THERE WILL COME SOFT RAINS” | Edith Södergran’s ON FOOT I HAD TO… | Robert Graves’s WELSH INCIDENT | Nancy Cunard’s ZEPPELINS | D.H. Lawrence’s WELLSIAN FUTURES | & many more.